Multi-Robot
Motion Planning
with Diffusion Models

Yorai Shaoul*, Itamar Mishani*, Shivam Vats*, Jiaoyang Li, and Maxim Likhachev

Coordinating Multiple Robots

What we want to do

  • Plan coordinated motions for multiple robots
  • With robots following data-driven motion patterns

Moley Robotics.

Teach skills via demonstrations.

Learn motion preferences from

collected data.

Coordinating Multiple Robots

Amazon Robotics

This work.

"Conveyor"

"Highways"

Freespace

"Drop-Region"

Coordinating Multiple Robots

What we want to do

 

Given

  • a set of robots \(\{\mathcal{R}_i\}_{i=1}^n\)
    sharing a workspace (\(\in\mathbb{R}^2\) or \(\in\mathbb{R}^3\) )
  • a motion dataset

Compute

  • A set of collision-free trajectories \(\{\boldsymbol{\tau}^i\}_{i=1}^n\)
    that adhere to the motion patterns 
    exhibited by the dataset

Motion Pattern

Coordinating Multiple Robots

Options to Tackle the Problem

Available
Data

Expressive Modeling

Scale with Agents

Scale to large environments

Learn directly [Carvalho et al. 2023]

Coordinating Multiple Robots

Options to Tackle the Problem

Available
Data

Expressive Modeling

Scale with Agents

Scale to large environments

Learn directly [Carvalho et al. 2023]

Learn cost maps for

classical planning

Coordinating Multiple Robots

Options to Tackle the Problem

What we want:  Rely on local, single-robot data,

and model flexibly

Learn directly [Carvalho et al. 2023]

Available
Data

Expressive Modeling

Scale with Agents

Scale to large environments

Learn cost maps for

classical planning

Coordinating Multiple Robots

How we do it 

Coordinate
single-robot planning diffusion models

with insights from
multi-agent path finding.

1
2

Background: Constraint-Based Multi-Agent Path Finding

​Extensive research on the Multi-Agent Path Finding (MAPF) problem has yielded strong algorithms.

Many algorithms impose constraints on single-robot planners.

For example, Conflict-Based Search (CBS) identifies collisions and re-plans for affected robots under new constraints.

1

Background: Constraint-Based Multi-Agent Path Finding

For example, Conflict-Based Search (CBS) identifies collisions and re-plans for affected robots under new constraints.

t=4
t=4
t=4
1

Background: Constraint-Based Multi-Agent Path Finding

For example, Conflict-Based Search (CBS) identifies collisions and re-plans for affected robots under new constraints.

t=4
t=4
t=4
t=4
t=4
1

Can we use these coordination ideas for robots that learn their motions?

Background: Diffusion Models

Motion Planning Diffusion models [Carvalho 2023, Janner 2022] generate trajectories from noisy trajectories.

Generate samples from noise.

2

Carvalho et al. 2023

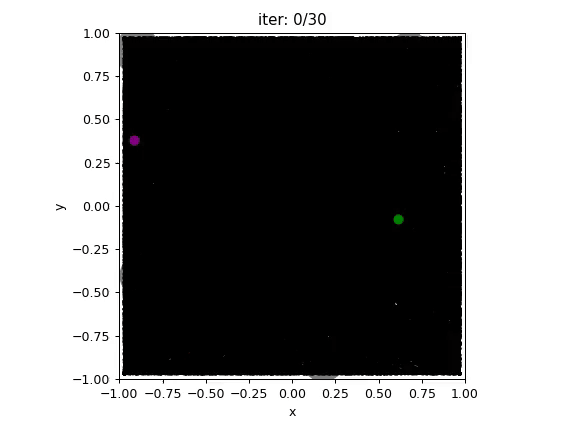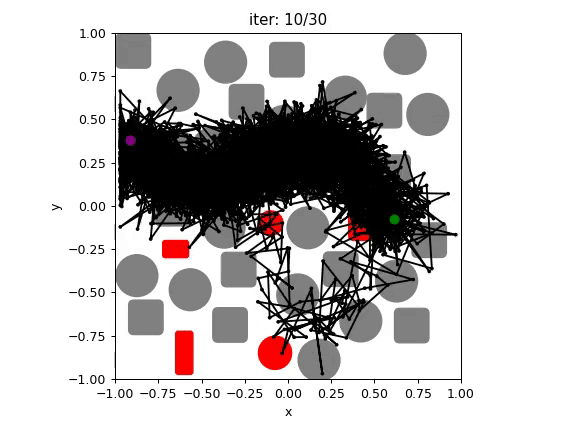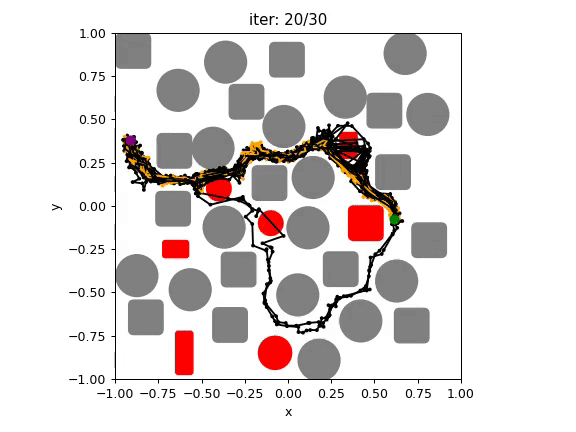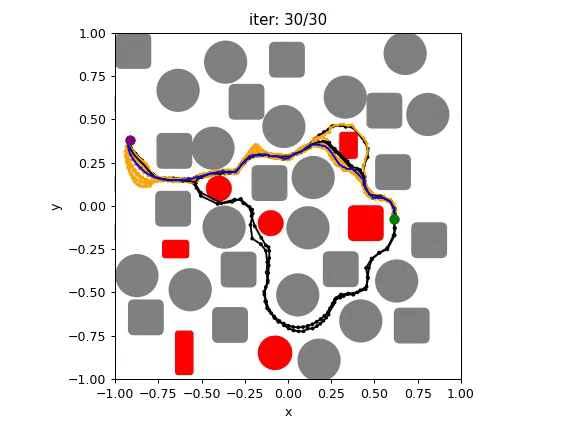
Dataset

Generated

Background: Diffusion Models

Motion Planning Diffusion models [Carvalho 2023, Janner 2022] generate trajectories from noisy trajectories.

2

Beginning from a pure noise trajectory \(^K\boldsymbol{\tau}^i\),
the model de-noises it incrementally for \(K\) denoising steps.

\underbrace{^K\boldsymbol{\tau}^i}_{\text{Pure noise}} \quad \rightarrow ^{K-1}\boldsymbol{\tau}^i \quad \rightarrow ^{K-2}\boldsymbol{\tau}^i \quad \rightarrow \cdots \rightarrow ^{1}\boldsymbol{\tau}^i \quad \rightarrow \underbrace{^{0}\boldsymbol{\tau}^i}_\text{Denoised}

Background: Diffusion Models

Motion Planning Diffusion models [Carvalho 2023, Janner 2022] generate trajectories from noisy trajectories.

2
\underbrace{^K\boldsymbol{\tau}^i}_{\text{Pure noise}} \quad \rightarrow ^{K-1}\boldsymbol{\tau}^i \quad \rightarrow ^{K-2}\boldsymbol{\tau}^i \quad \rightarrow \cdots \rightarrow ^{1}\boldsymbol{\tau}^i \quad \rightarrow \underbrace{^{0}\boldsymbol{\tau}^i}_\text{Denoised}
\mu^i_{k-1} \gets \mu^i_\theta(^{k}\boldsymbol{\tau}^i)

Denoising Process

Background: Diffusion Models

Motion Planning Diffusion models [Carvalho 2023, Janner 2022] generate trajectories from noisy trajectories.

^{k-1}\boldsymbol{\tau}^i \sim \mathcal{N} \left( \mu^i_{k-1} , \beta_{k-1} \right)
2
\underbrace{^K\boldsymbol{\tau}^i}_{\text{Pure noise}} \quad \rightarrow ^{K-1}\boldsymbol{\tau}^i \quad \rightarrow ^{K-2}\boldsymbol{\tau}^i \quad \rightarrow \cdots \rightarrow ^{1}\boldsymbol{\tau}^i \quad \rightarrow \underbrace{^{0}\boldsymbol{\tau}^i}_\text{Denoised}
\mu^i_{k-1} \gets \mu^i_\theta(^{k}\boldsymbol{\tau}^i)

Denoising Process

Background: Diffusion Models

Motion Planning Diffusion models [Carvalho 2023, Janner 2022] generate trajectories from noisy trajectories.

^{k-1}\boldsymbol{\tau}^i \sim \mathcal{N} \left( \mu^i_{k-1} , \beta_{k-1} \right)
2
\underbrace{^K\boldsymbol{\tau}^i}_{\text{Pure noise}} \quad \rightarrow ^{K-1}\boldsymbol{\tau}^i \quad \rightarrow ^{K-2}\boldsymbol{\tau}^i \quad \rightarrow \cdots \rightarrow ^{1}\boldsymbol{\tau}^i \quad \rightarrow \underbrace{^{0}\boldsymbol{\tau}^i}_\text{Denoised}
\mu^i_{k-1} \gets \mu^i_\theta(^{k}\boldsymbol{\tau}^i)

Denoising Process

Background: Diffusion Models

Motion Planning Diffusion models [Carvalho 2023, Janner 2022] generate trajectories from noisy trajectories.

2
\underbrace{^K\boldsymbol{\tau}^i}_{\text{Pure noise}} \quad \rightarrow ^{K-1}\boldsymbol{\tau}^i \quad \rightarrow ^{K-2}\boldsymbol{\tau}^i \quad \rightarrow \cdots \rightarrow ^{1}\boldsymbol{\tau}^i \quad \rightarrow \underbrace{^{0}\boldsymbol{\tau}^i}_\text{Denoised}
\mu^i_{k-1} \gets \mu^i_\theta(^{k}\boldsymbol{\tau}^i)

Denoising Process

^{k-1}\boldsymbol{\tau}^i \sim \mathcal{N} \left( \mu^i_{k-1} + \underbrace{\eta \beta_{k-1} \nabla_{\boldsymbol{\tau}} \mathcal{J}(\mu^i_{k-1})}_{\text{Guidance}}, \beta_{k-1} \right)

Background: Diffusion Models

2
\mu^i_{k-1} \gets \mu^i_\theta(^{k}\boldsymbol{\tau}^i)

Denoising Process

^{k-1}\boldsymbol{\tau}^i \sim \mathcal{N} \left( \mu^i_{k-1} + \underbrace{\eta \beta_{k-1} \nabla_{\boldsymbol{\tau}} \mathcal{J}(\mu_{k-1})}_{\text{Guidance}}, \beta_{k-1} \right)

Allows us to design "soft" spatio-temporal constraints via guidance functions.

MMD Multi-Robot Multi-Model Diffusion Planning

In this work, we draw on ideas from MAPF algorithms to coordinate learned motion planners.

Example: MMD-CBS

t=32

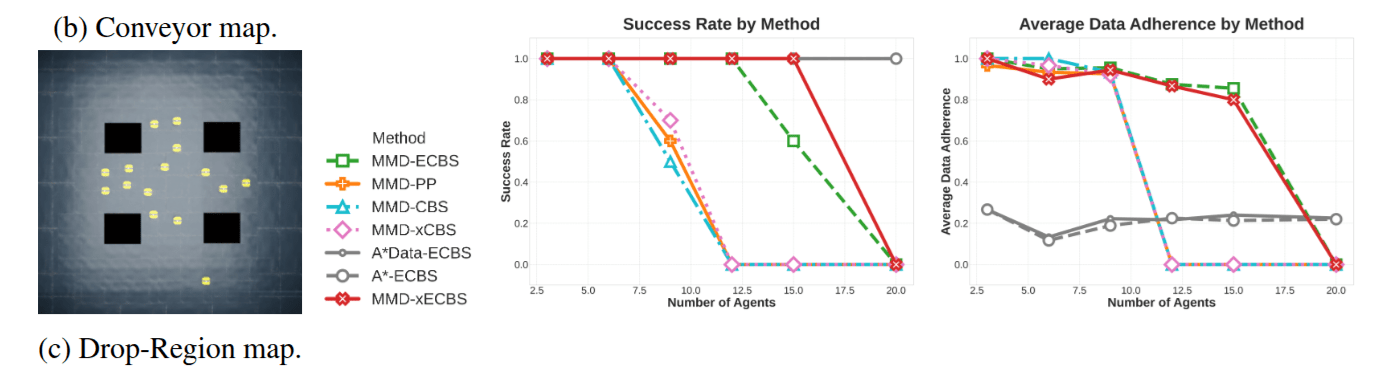
MMD: Results

What we would like to see:

The higher success-rate, the better.

...without compromising data adherence.

Number of Agents

Success Rate

Number of Agents

Data Adherence

MMD: Results

A naive application of CBS is insufficient.

Easy

Hard

MMD: Results

A naive application of CBS is insufficient, and ideas from improved algorithms help.

 

Easy

Hard

MMD: Results

A naive application of CBS is insufficient, ideas from improved algorithms helped, and baselines struggled.

 

Easy

Hard

MMD: Results

Please refer to our paper for more results.

Easy

Hard

MMD: Larger Environments

MMD learns single-robot models for small, easy-to-learn, sub-environments and composes those to scale in space and time as well. 

Multi-Robot Motion Planning with Diffusion Models 

MMD leverage the structure of diffusion models, and ideas from MAPF algorithms, to enable data-driven multi-robot motion planning.

multi-robot-diffusion.github.io
t=32